1. Aturan Sinus dalam Segitiga
Pada segitiga di atas berlaku
loh, darimana asalnya aturan sinus tersebut? mari kita cari tahu pembuktiannya berikut
pembuktian aturan sinus paling mudah melalui pendekatan pembuktian dari rumus luas segitiga. Silahkan baca pembuktian rumus luas segitiga di bagian akhir postingan ini terlebih dahulu. Menurut aturan luas segitiga di dapat
L = ½ bc. sin α … (1)
L = ½ ac. sin β … (2)
L = ½ ab. sin γ … (3)
Persamaan (1) dan (2)pembuktian aturan sinus paling mudah melalui pendekatan pembuktian dari rumus luas segitiga. Silahkan baca pembuktian rumus luas segitiga di bagian akhir postingan ini terlebih dahulu. Menurut aturan luas segitiga di dapat
L = ½ bc. sin α … (1)
L = ½ ac. sin β … (2)
L = ½ ab. sin γ … (3)
L = L
½ bc. sin α = ½ ac. sin β (coret yang sama)
b sin α = a sin β
b/sin β = a/sin α
Persamaan (1) dan (3)
L = L
½ bc. sin α = ½ ab. sin γ
c. sin α = a sin γ
c/sin γ = a/sin α
nah terbukti kan aturan sinus segitiganya.
contoh soal
Misalkan pada segitiga ABC, ∠ A =30o, BC = 6 dan AC = 10, tentukan berapa besar ∠B
jawab :
BC/sin A = AC/ sin B
6/ sin 30o = 10/ sin B
6/ 0,5 = 10 / sin B
12 = 10/sin B
sin B = 10/12 = 5/6
maka sudut B adalah 56,44o
BC/sin A = AC/ sin B
6/ sin 30o = 10/ sin B
6/ 0,5 = 10 / sin B
12 = 10/sin B
sin B = 10/12 = 5/6
maka sudut B adalah 56,44o
2. Atuan Cosinus dalam Segitiga
Pasa sebuah segitiga dengan titik sudut A, B, C, panjang sisi a,b,c, dan sudut α, β, γ berlaku aturan cosinus
a2 = b2 + c2 – 2bc cos α
b2 = a2 + c2 – 2ac cos β
c2 = a2 + b2 – 2ab cos γ
b2 = a2 + c2 – 2ac cos β
c2 = a2 + b2 – 2ab cos γ
Pembuktian aturan cosinus
Darimana dapatnya aturan cosinus di atas? Jawabannya adalah
c2 = (a sin γ)2 + (b-a cos γ)2
c2 = a2 sin2 γ + b2- 2ab cos γ + a2 cos2 γ
c2 = a2 sin2 γ + a2 cos2 γ + b2- 2ab cos γ
c2 = a2 (sin2 γ + cos2 γ) + b2- 2ab cos γ (ingat sobat sin2 a + cos2 a = 1)
c2 = a2+ b2- 2ab cos γ… (terbukti)
contoh soalc2 = a2 sin2 γ + b2- 2ab cos γ + a2 cos2 γ
c2 = a2 sin2 γ + a2 cos2 γ + b2- 2ab cos γ
c2 = a2 (sin2 γ + cos2 γ) + b2- 2ab cos γ (ingat sobat sin2 a + cos2 a = 1)
c2 = a2+ b2- 2ab cos γ… (terbukti)
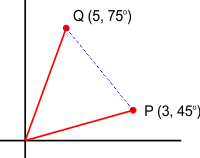
perhatikan gambar di samaping. Titik P dan Q dinyatakan dengan korrdinat polar. Tentukan jarak antar titik Pdan Q.
Jawab:
Dari gambar di atas terlihat bentuk segitiga dan jarak antar titik P dan Q bisa dicari dengan menggunakan aturan cosinus.
Besar sudut POQ = 180o – (75o+45o) = 60o.
PQ2 = OQ2 + OP2 – 2.OQ.OP cos ∠POQ
PQ2 = 32 + 52 – 2.3.5 cos 60o c
PQ2 = 9 + 25 – 30. 0,5
PQ2 = 9 + 25 -15
PQ2 = 19
PQ = √19 = 4,36
3. Aturan Trigonometri Luas Segitiga
Selain aturan sinus dan cosinus dalam segitiga berlaku rumus luas segitiga menggunakan aturan trigonometri.
Jika sobat punya sebuah segitiga seperti gambar di bawah ini
Jika sobat punya sebuah segitiga seperti gambar di bawah ini
Luas Segitiga ABC
= ½ bc. sin α
= ½ ac. sin β
= ½ ab. sin γ
= ½ bc. sin α
= ½ ac. sin β
= ½ ab. sin γ
Eh..eh.. dari mana dapetnya rumus tersebut? The proof is..
pembuktian rumus ini sangat mudah jika sobat punya sebuah segitiga sembarang seperti ini
pembuktian rumus ini sangat mudah jika sobat punya sebuah segitiga sembarang seperti ini
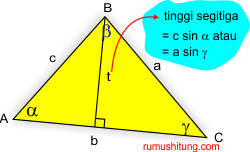
perhatikan segitiga di atas, rumus luas
segitiga adalah ½ x alas x tinggi. Kita ganti nilai tinggi dengan c sin α
atau a sin γ maka didapat
L = ½ b. c. sin α atau
L = ½ b. a. sin γ
Gampang kan sebenarnya. Hehehe
contoh soalL = ½ b. c. sin α atau
L = ½ b. a. sin γ
Gampang kan sebenarnya. Hehehe
Jika sobat rumushitung berikan selembar karton warna ungu dengan bentuk segitiga seperti gambar berikut
coba sobat tentukan luas segitiga tersebut
Luas segitiga = ½ 3.5. sin 30o = ½.3.5.½ = 15/4 = 3,75 cm
Ayo sobat hitung, buat melatih pemahaman kita tentang aturan
trigonometri (aturan sinus, aturan cosinus, dan aturan luas) segitiga
boleh dicoba latihan soal berikut:Luas segitiga = ½ 3.5. sin 30o = ½.3.5.½ = 15/4 = 3,75 cm
1. Perhatikan gambar segitiga di bawah ini lalu tentukan perbandingan antara PQ dan PR

a. 4 : 3 b. 3 : 4
c. √3 : √2 d. √2 : √3
2. Luas dari segitiga di bawah ini adalah?
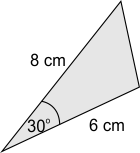
a. 12 cm2 b. 12√3 cm2
c. 12 √2 cm2 d. 14 cm2
3. Pada gambar di samping tentukan nilai dari x
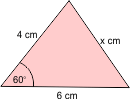
a. 2√3 b. 2√10
c. 2√7 d. 2√5
sumber : http://rumushitung.com
Sign up here with your email
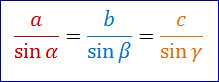


ConversionConversion EmoticonEmoticon